Buen dia, nuestro tema de hoy será la compensación por presión y temperatura de la variable flujo de vapor que que ha sido tratada y acondicionada en los dos capítulos anteriores Escalización de variables en AB ControlLogix parte II y Escalización de variables en AB ControlLogix parte III.
Importancia de la compensación dinámica para el cálculo de flujo másico
La norma ISO 5167-2 para la medición de flujo nos expresa en su capítulo 4 que el caudal másico se puede determinar usando la siguiente ecuación:
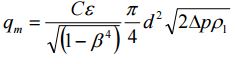
Donde:
Qm = Caudal másico (Kg/s)
C = Coeficiente de descarga
ε = Factor de expansión
B = Relación de diámetros de la platina orificio (d/D).
π = Constante universal 3.14159
ΔP = presión diferencial a través de la platina orificio (Pa)
ρ1 = Densidad del fluido (Kg/m3)
Las variables dinámicas para el cálculo de flujo másico como lo son la densidad, el coeficiente de descarga, el factor de expansión y la misma presión diferencial son de alta dependencia de la presión y temperatura del proceso, por eso es aquí donde la importancia de compensar por presión y temperatura se hace necesario y es por tal motivo que en nuestro siguiente diagrama SAMA correspondiente a nuestro control de nivel por tres elementos aparece representado en el circulo amarillo.
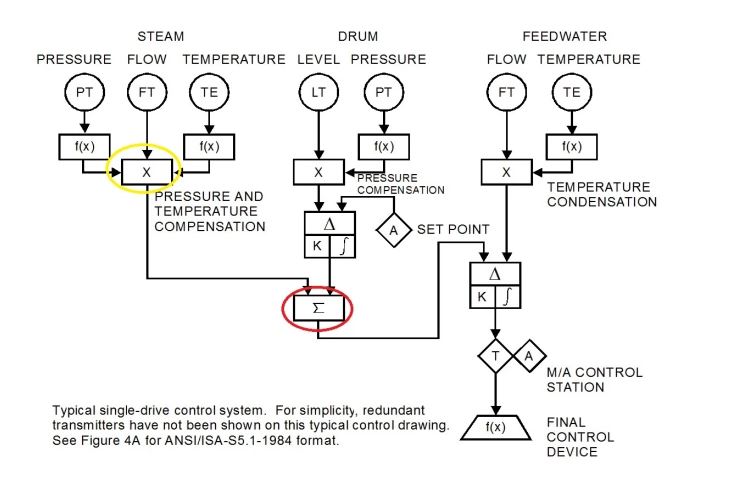
Compensación de presión y temperatura para determinar el flujo másico de vapor en Rslogix 5000
A continuación veremos los bloques y cálculos requeridos para llevar a cabo la compensación dinámica. Recordemos que el dato FLOW_CALC_403 fue tratado en el capítulo anterior por lo cual omitiremos detalles y mejor nos centraremos en el dato SH_TT_PT_CALC.
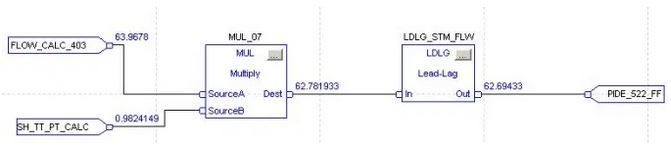
El dato SH_TT_PT_CALC Este dato usado como compensación dinámica es el resultado de lo siguiente:
Inicialmente empezaremos por la señal de temperatura AI_TT_407, que ha sido escalizada de la siguiente manera, y del mismo modo que ya lo hemos visto anteriormente.
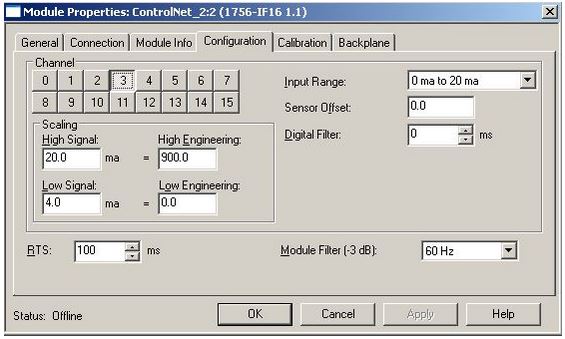
Esta señal de temperatura tiene tres ramificaciones, la primera es dirigida a un generador de funciones FGEN_TT_407, la segunda va hacia un bloque de comparación LES_08 (Menor que) y la tercera es direccionada a otro comparador GRT_07 (Mayor que).
El generador de funciones FGEN_TT_407 convierte una entrada basada en una función lineal por tramos.
Ahora vamos a explorar el bloque generador de funciones para una mejor interpretación.
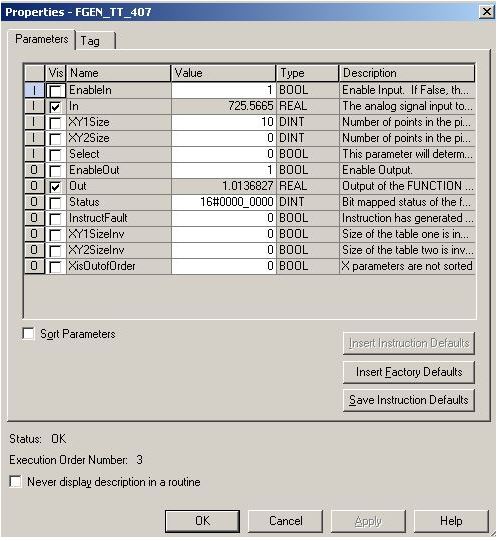
In: Es una señal analogica, en este caso es proveniente de la señal de temperatura de vapor.
XY1Size: Es el número de puntos de la curva de la tabla #1, tanto para el eje X como el Y que en nuestro caso es 10.
XY2Size: Es el número de puntos de la curva de la tabla #2, tanto para el eje X como el Y, en este caso no tendremos la necesidad de otra tabla, asi que su valor sera 0.
Select: Es un dato booleano, donde determinamos qué tabla usar. Si el valor en este parámetro es 0, la tabla a usar será la 1 (XY1), si el valor es 1 la tabla a usar es la 2 (XY2).
Out: Es la salida ante la respuesta del cálculo ejecutado por la tabla con los valores introducidos.
Nuestro bloque por otro lado requiere de la creación de dos datos de memoria para el almacenamiento de las 10 entradas X y las 10 salidas Y.
#6. Datos de entrada y de salida del bloque.
Ahora las 10 entradas o memorias del eje X, son almacenadas en value y a cada una se le ha definido un valor.
#7. Valores de entrada X desde monitor tags.
Y aquí las 10 salidas o memorias del eje Y, son almacenadas en value y a cada una se le ha definido otro valor.
#8. Valores de entrada Y desde monitor tags.
Por ultimo aqui es visualizada la respuesta de ambas señales, donde para un cambio en X, habrá un cambio en Y.

#9. Curva de caracterización.
Las instrucciones usada por el algoritmo son las siguientes:
Cuando In ≤ X[1] entonces la salida = Y[1]
Por ejemplo si la entrada es de 450 °C :
Cuando 450°F ≤ 500°F entonces la salida = 1.207
Recordemos que en los valores de entrada para X (figura 7) en la posición X[1], hemos cargado un valor de 500 y en los valores de entrada para Y (figura 8) en la posición Y[1], hemos cargado un valor de 1.207.
Cuando In > X[XY<n>Size] entonces la salida = Y[XY<n>Size]
Por ejemplo si la entrada es de 1200 °C (Cosa que nunca pasará pues nuestro rango es hasta 900°F, ver figura 2) :
Cuando 1200°F > 1000°F entonces la salida = 0.894
Recordar que el tamaño X[XY<n>Size] es de 10 (ver figura 5, propiedades del bloque). Ahora recordemos que en la posición 10 de nuestra tabla para el eje X (figura 7), tenemos un valor de 1000 y en la posición 10 de nuestra tabla Y (figura 8), tenemos un valor de 0.984.
Cuando X[n] < In ≤ X[n + 1], entonces la salida será:
((Y[n+1]-Yn) / (X[n+1]-Xn)) * (In-Xn)+Yn
Por ejemplo si 550°F < 600°f ≤ 600°F entonces la salida
=((1,098-1,145)/(600-550))*(600-550)+1,145
Cuando mencionamos Y[n+1], debemos centrar nuestra atención al dato que tenemos en el eje X, recordar que para nuestro ejemplo nuestro dato es de 550°F, que corresponde a la posición X[2]. Ahora en la posición [2] pero en el eje Y encontramos un dato de 1.145, pero como la condición de nuestro algoritmo es sumarle un uno a la posición actual de Y (Y[n+1]), entonces ya nuestro dato sería Y[3] que es igual a un valor de 1,098.
Yn es el dato de Y para una posición definida en X. Como lo mencionamos anteriormente X se encuentra en 550°F el cual su posición es [2], en la misma posición [2] pero en el eje Y se encuentra un valor de 1.145.
X[n+1], equivale a la suma de una posición en el eje X, quiere decir que como en el eje X nuestro valor es de 550°F en la posición [2] , es necesario sumarle una posición quedando en X[3] y ahora correspondiendo a un valor de 600°F.
Xn corresponde a la posición actual de X, 550.
In, es la señal análoga de entrada en el bloque.
Nota:
Ahora como ya sabemos la operación del bloque de generador de funciones, quiero comentarte que los datos ingresados tanto en el eje X, como en el eje Y son propios datos ya proporcionados por el fabricante de la caldera, que se ha dado a la tarea de realizar complejos cálculos para determinar la influencia de la temperatura en el flujo de vapor de salida de la caldera.
SEL_34
El selector marcado en amarillo, cumple la función de garantizar una señal estática en caso de un fallo en la señal de temperatura por posibles problemas el transmisor.

#9. Bloque SEL_34.
Cabe resaltar nuevamente que este bloque posee una entrada de señal analogica y otra de tipo booleano); si la señal booleana está presente (1), la salida del bloque será un dato estático cargado en las propiedades del bloque (In2) que corresponde a un valor de 1. Sí de modo contrario la señal booleana está en false (0), la salida de nuestro bloque será igual a la entrada.

#10. Propiedades del bloque SEL_34
Falla del transmisor de temperatura
En la zona delimitada en amarillo, están los bloques usados para determinar la falla del transmisor de temperatura, a su vez el resultado final de todos estos bloque es usado como dato booleano hacia el selector mencionado anteriormente.
#11. Falla del transmisor.
Los bloques encargados para determinar la falla del transmisor de temperatura son el LES_08 y el GRT_07.
El bloque LES_08, compara la señal de entrada (SourceA), si esta es menor a un dato establecido internamente de 0°F en (SourceB), me indicará mediante a un dato booleano (true) que la corriente del transmisor a disminuido a un punto inferior a los 4 mA.

#12. Propiedades del bloque LES_08.
El bloque GRT_07, compara la señal de entrada (SourceA), si esta es mayor a un dato establecido internamente de 1000°F en (SourceB), me indicará mediante a un dato booleano (true) que la corriente del transmisor a superado a el punto máximo de 20 mA.

#13. Propiedades del bloque GRT_07
Por último el bloque BOR_08 no es nada más que una compuerta lógica Or la cual requiere de que cualquiera de sus entradas está activa para que su salida también lo sea, tal y como lo muestra la siguiente imagen:

Para finalizar, la salida de nuestra compuerta lógica OR (BOR_08), irá hacia el bloque SEL_34 mencionado anteriormente y será el resultado de nuestra implementación para la detección de fallas en el transmisor el cual podrá usarse en otras secciones para informar al operador de que algo no anda bien, hacer parte de un control donde esta falla sea la causa de un efecto, entre otras alternativas.

Conclusión final
Hemos comentado con gran detalle el funcionamiento del generador de funciones que puede ser usado en múltiples aplicaciones donde se requiera una respuesta relacionada a unos datos de entrada, hemos analizado nuevamente como el bloque SEL donde su aplicación es extensa y en distintos procesos y hemos explorado opciones con bloques de comparación para la determinación de una falla en un transmisor.








